基本信息

评测编号	025
论文名称	基于ISM的高职学生顶岗实习满意度影响因素分析
作者	白玲
通讯方式	，辽宁师范大学教育学院2015级博士研究生
原始文章	基于ISM的高职学生顶岗实习满意度影响因素分析

从最终层级图进行初步判断

论文原始截图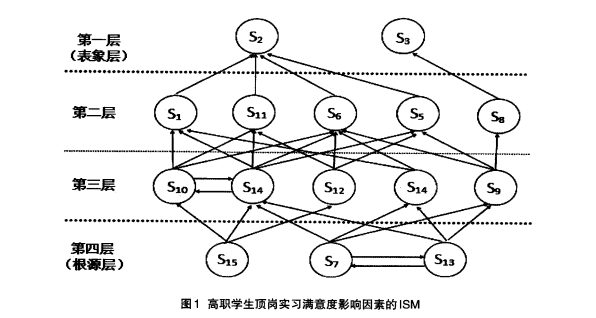
同一层级是否有横向非回路箭头	无
初步评估结果	无
说明	很漂亮的层级。

从原始矩阵开始根据文章采用的方法进行计算

原始矩阵=

$$原始矩阵A=\begin{vmatrix}0&0&0&0&0&0&0&0&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0&0&0&0&0&0&0&0\\ 1&0&0&0&1&1&0&0&1&0&1&1&1&0&1\\ 1&1&0&0&1&0&0&1&0&1&0&0&0&1&1\\ 1&1&0&0&0&1&1&0&0&0&0&0&0&0&1\\ 1&1&1&0&1&0&1&1&0&0&0&0&1&0&1\\ 1&1&0&0&0&1&0&0&0&0&0&0&0&0&1\\ 1&1&1&1&1&1&0&0&1&1&0&0&0&0&1\\ 1&1&1&1&1&1&0&1&0&0&0&0&0&0&1\\ 1&0&0&0&0&0&0&1&1&0&0&0&0&0&0\\ 1&1&1&1&0&1&0&1&0&1&0&0&0&0&0\\ 1&1&1&1&0&1&0&1&0&1&0&0&0&0&0\\ 1&0&0&1&1&1&0&0&1&0&0&1&0&1&1\\ 0&1&1&0&0&0&1&0&1&0&0&0&1&0&0\\ 1&1&1&0&0&0&1&1&1&0&0&0&1&1&0\\\end{vmatrix} $$

计算结果比较

$$可达矩阵R=\begin{vmatrix}1&0&0&0&0&0&0&0&0&0&0&0&0&0&0\\ 1&1&0&0&0&0&0&0&0&0&0&0&0&0&0\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\ 1&1&1&1&1&1&1&1&1&1&1&1&1&1&1\\\end{vmatrix} $$$$缩减矩阵S=\begin{vmatrix}0&0&0&0&0&0&0&0&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0&0&0&0&0&0&0&0\\ 0&0&0&1&0&0&0&0&0&0&0&0&0&0&0\\ 0&1&0&0&1&0&0&0&0&0&0&0&0&0&0\\ 0&0&0&0&0&1&0&0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&1&0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&1&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&1&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&0&1&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&0&0&1&0&0&0&0\\ 0&0&0&0&0&0&0&0&0&0&0&1&0&0&0\\ 0&0&0&0&0&0&0&0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&0&0&0&0&0&0&0&1&0\\ 0&0&0&0&0&0&0&0&0&0&0&0&0&0&1\\ 0&0&1&0&0&0&0&0&0&0&0&0&0&0&0\\\end{vmatrix} $$

原始结果

第0层

第1层

第2层

结论：错误

正确的结果是团成一团，是一个大回路！这个原始矩阵都歪歪扭扭，作者显然不大会排版。

想在线计算解释结构模型的或者直接生成论文的请发电子邮件到， hwstu #sohu.com 把#替换成 @