基本信息

评测编号	040
论文名称	基于解释结构模型的风电产业价值驱动因素分析
作者	刘吉成，付晓旭，何丹丹，王刚
通讯方式	华北电力大学经济与管理学院，北京 102206
原始文章	基于解释结构模型的风电产业价值驱动因素分析

从最终层级图进行初步判断

论文原始截图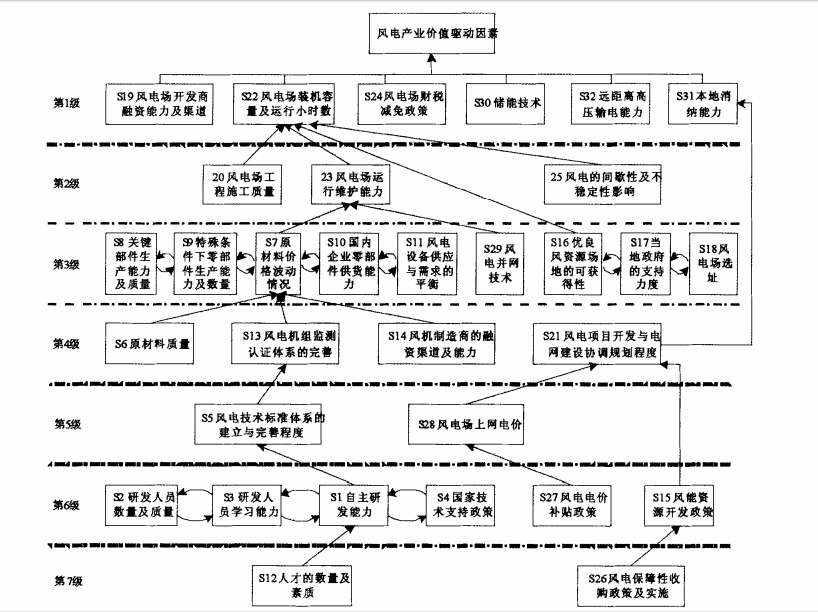
同一层级是否有横向非回路箭头	无
初步评估结果	无
说明	发现该学校好像很喜欢用这个模型，看到好多篇用ISM的文章。

从原始矩阵开始根据文章采用的方法进行计算

原始矩阵=

$$原始矩阵A=\begin{array} {c|ccccccc}{M_{32 \times32}} &1 &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12 &13 &14 &15 &16 &17 &18 &19 &20 &21 &22 &23 &24 &25 &26 &27 &28 &29 &30 &31 &32\\ \hline 1 &0 &1 &1 &1 &1 &0 &0 &1 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &0\\ \hline 2 &1 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &0\\ \hline 3 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 4 &1 &1 &1 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 5 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &1 &0 &0 &0 &0 &0 &0 &1 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 6 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 7 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 8 &0 &0 &0 &0 &0 &0 &1 &0 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 9 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 10 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 11 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 12 &1 &0 &1 &0 &0 &0 &0 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 13 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 14 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 15 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &1 &0 &1 &1 &0 &1 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 16 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 17 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 18 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0\\ \hline 19 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 20 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 21 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1\\ \hline 22 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 23 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 24 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 25 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 26 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 27 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0\\ \hline 28 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 29 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 30 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 31 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 32 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline \end{array} $$

计算结果比较

$$可达矩阵R=\begin{array} {c|ccccccc}{M_{32 \times32}} &1 &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12 &13 &14 &15 &16 &17 &18 &19 &20 &21 &22 &23 &24 &25 &26 &27 &28 &29 &30 &31 &32\\ \hline 1 &1 &1 &1 &1 &1 &0 &1 &1 &1 &1 &1 &0 &1 &0 &0 &1 &1 &1 &0 &1 &0 &1 &1 &0 &0 &0 &0 &0 &1 &1 &1 &0\\ \hline 2 &1 &1 &1 &1 &1 &0 &1 &1 &1 &1 &1 &0 &1 &0 &0 &1 &1 &1 &0 &1 &0 &1 &1 &0 &0 &0 &0 &0 &1 &1 &1 &0\\ \hline 3 &1 &1 &1 &1 &1 &0 &1 &1 &1 &1 &1 &0 &1 &0 &0 &1 &1 &1 &0 &1 &0 &1 &1 &0 &0 &0 &0 &0 &1 &1 &1 &0\\ \hline 4 &1 &1 &1 &1 &1 &0 &1 &1 &1 &1 &1 &0 &1 &0 &0 &1 &1 &1 &0 &1 &0 &1 &1 &0 &0 &0 &0 &0 &1 &1 &1 &0\\ \hline 5 &0 &0 &0 &0 &1 &0 &1 &1 &1 &1 &1 &0 &1 &0 &0 &0 &0 &0 &0 &1 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 6 &0 &0 &0 &0 &0 &1 &1 &1 &1 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 7 &0 &0 &0 &0 &0 &0 &1 &1 &1 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 8 &0 &0 &0 &0 &0 &0 &1 &1 &1 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 9 &0 &0 &0 &0 &0 &0 &1 &1 &1 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 10 &0 &0 &0 &0 &0 &0 &1 &1 &1 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 11 &0 &0 &0 &0 &0 &0 &1 &1 &1 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 12 &1 &1 &1 &1 &1 &0 &1 &1 &1 &1 &1 &1 &1 &0 &0 &1 &1 &1 &0 &1 &0 &1 &1 &0 &0 &0 &0 &0 &1 &1 &1 &0\\ \hline 13 &0 &0 &0 &0 &0 &0 &1 &1 &1 &1 &1 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 14 &0 &0 &0 &0 &0 &0 &1 &1 &1 &1 &1 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 15 &0 &0 &0 &0 &0 &0 &1 &1 &1 &1 &1 &0 &0 &1 &1 &1 &1 &1 &1 &0 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1\\ \hline 16 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &1 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0\\ \hline 17 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &1 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0\\ \hline 18 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &1 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0\\ \hline 19 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 20 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 21 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1\\ \hline 22 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 23 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 24 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 25 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0\\ \hline 26 &0 &0 &0 &0 &0 &0 &1 &1 &1 &1 &1 &0 &0 &1 &1 &1 &1 &1 &1 &0 &1 &1 &0 &0 &0 &1 &0 &0 &0 &0 &1 &1\\ \hline 27 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &1 &0 &0 &1 &1 &0 &0 &0 &0 &1 &1 &0 &0 &1 &1\\ \hline 28 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &1 &0 &0 &1 &1 &0 &0 &0 &0 &0 &1 &0 &0 &1 &1\\ \hline 29 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &0 &0 &0 &0 &1 &0 &0 &0\\ \hline 30 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0\\ \hline 31 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0\\ \hline 32 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1\\ \hline \end{array} $$$$缩减矩阵S=\begin{array} {c|ccccccc}{M_{32 \times32}} &1 &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12 &13 &14 &15 &16 &17 &18 &19 &20 &21 &22 &23 &24 &25 &26 &27 &28 &29 &30 &31 &32\\ \hline 1 &0 &1 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1 &0 &0\\ \hline 2 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 3 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 4 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 5 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 6 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 7 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 8 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 9 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 10 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 11 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 12 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 13 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 14 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 15 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &1 &0 &0 &1 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 16 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 17 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 18 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0\\ \hline 19 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 20 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 21 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &1 &1\\ \hline 22 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 23 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 24 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 25 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 26 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 27 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0\\ \hline 28 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 29 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &1 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 30 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 31 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline 32 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0 &0\\ \hline \end{array} $$

原始结果

结论：错误

看这个矩阵真心的累，不过这么大的矩阵，很少人愿意去核实的。也很难去核对的。一不小心就手抖。极有可能按照其原始矩阵输入后有遗漏。这个要特此说明一下。也非常有可能其排版的时候少了某个1。

想在线计算解释结构模型的或者直接生成论文的请发电子邮件到， hwstu #sohu.com 把#替换成 @