DEMATEL-AHDT-WEIGHT在线计算
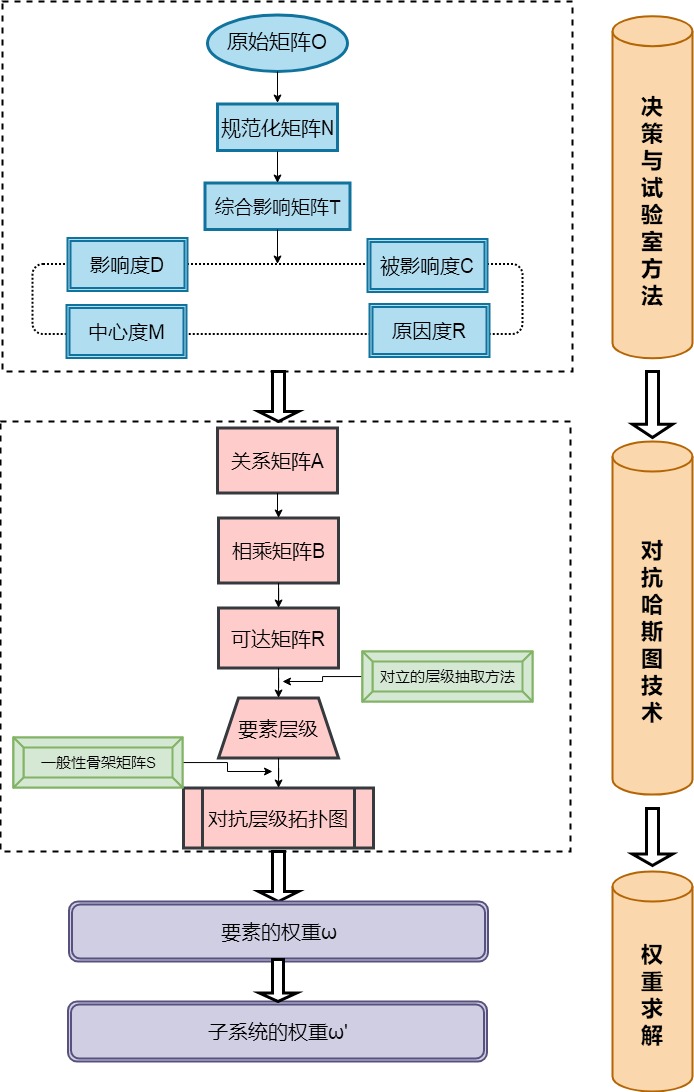
流程图
原始矩阵为
$$Ori=\begin{array}{|c|c|c|c|c|c|c|}\hline {M_{20 \times20}} &A1 &A2 &A3 &B1 &B2 &B3 &C1 &C2 &C3 &C4 &D1 &D2 &D3 &D4 &D5 &E1 &E2 &E3 &E4 &E5\\ \hline A1 &0 &2 &6 &16 &2 &36 &48 &7 &1 &14 &18 &3 &20 &48 &47 &15 &19 &8 &1 &25\\ \hline A2 &13 &0 &12 &35 &8 &11 &36 &12 &34 &13 &36 &24 &11 &23 &35 &12 &13 &9 &5 &48\\ \hline A3 &1 &1 &0 &29 &3 &18 &2 &11 &1 &2 &36 &48 &3 &8 &1 &4 &36 &1 &3 &9\\ \hline B1 &1 &1 &2 &0 &12 &35 &14 &15 &16 &29 &31 &13 &13 &14 &16 &38 &16 &27 &14 &19\\ \hline B2 &1 &2 &3 &47 &0 &47 &47 &48 &1 &1 &9 &3 &36 &48 &12 &47 &35 &10 &36 &47\\ \hline B3 &3 &3 &2 &9 &1 &0 &2 &2 &4 &3 &4 &1 &3 &36 &23 &35 &3 &3 &12 &1\\ \hline C1 &4 &3 &4 &4 &4 &4 &0 &2 &3 &3 &3 &3 &25 &21 &22 &48 &1 &2 &3 &4\\ \hline C2 &1 &3 &4 &5 &6 &7 &8 &0 &9 &18 &28 &11 &39 &47 &2 &48 &5 &6 &45 &4\\ \hline C3 &2 &4 &6 &36 &10 &37 &12 &11 &0 &37 &37 &12 &11 &20 &12 &37 &44 &27 &35 &24\\ \hline C4 &2 &4 &7 &9 &4 &4 &6 &4 &4 &0 &7 &3 &3 &3 &3 &28 &4 &37 &6 &37\\ \hline D1 &2 &3 &8 &3 &3 &3 &3 &3 &20 &35 &0 &37 &2 &2 &2 &30 &48 &48 &3 &7\\ \hline D2 &1 &3 &9 &2 &3 &14 &2 &10 &3 &3 &3 &0 &48 &3 &4 &5 &5 &11 &5 &5\\ \hline D3 &1 &3 &13 &2 &3 &6 &8 &6 &6 &6 &6 &7 &0 &2 &2 &2 &5 &4 &8 &5\\ \hline D4 &5 &23 &3 &3 &3 &5 &5 &5 &5 &4 &7 &5 &48 &0 &5 &24 &11 &11 &8 &8\\ \hline D5 &3 &2 &4 &6 &3 &36 &7 &8 &10 &11 &12 &13 &48 &3 &0 &7 &7 &9 &7 &7\\ \hline E1 &6 &12 &3 &4 &3 &3 &3 &3 &6 &3 &14 &3 &3 &3 &8 &0 &11 &11 &11 &11\\ \hline E2 &3 &2 &5 &3 &3 &3 &3 &9 &3 &3 &3 &13 &48 &20 &8 &48 &0 &7 &11 &11\\ \hline E3 &1 &2 &3 &23 &3 &36 &36 &36 &13 &37 &8 &8 &8 &29 &18 &48 &20 &0 &15 &11\\ \hline E4 &1 &4 &3 &3 &3 &14 &11 &10 &9 &8 &8 &16 &18 &8 &8 &48 &3 &12 &0 &30\\ \hline E5 &2 &5 &3 &23 &3 &24 &24 &24 &3 &36 &5 &3 &3 &4 &7 &36 &4 &4 &36 &0\\ \hline \end{array} $$
决策与实验室方法部分——DEMATEL部分
规范矩阵N $$ \require{cancel} \require{AMScd} \begin{CD} O @>>>N \\ \end{CD} $$
综合影响矩阵T $$ \begin{CD} N @>>>T \\ \end{CD} $$
综合影响矩阵T如下
求解$T=\mathcal{N}(I-\mathcal{N})^{-1}$
$$T=\begin{array}{|c|c|c|c|c|c|c|}\hline {M_{20 \times20}} &A1 &A2 &A3 &B1 &B2 &B3 &C1 &C2 &C3 &C4 &D1 &D2 &D3 &D4 &D5 &E1 &E2 &E3 &E4 &E5\\ \hline A1 &0.008 &0.019 &0.025 &0.054 &0.013 &0.108 &0.122 &0.036 &0.02 &0.059 &0.063 &0.03 &0.094 &0.132 &0.122 &0.1 &0.066 &0.046 &0.031 &0.078\\ \hline A2 &0.035 &0.015 &0.041 &0.107 &0.03 &0.075 &0.11 &0.058 &0.094 &0.076 &0.114 &0.083 &0.084 &0.091 &0.105 &0.116 &0.072 &0.063 &0.055 &0.139\\ \hline A3 &0.006 &0.01 &0.009 &0.073 &0.013 &0.059 &0.019 &0.039 &0.016 &0.027 &0.092 &0.118 &0.045 &0.04 &0.017 &0.056 &0.097 &0.028 &0.027 &0.038\\ \hline B1 &0.009 &0.016 &0.017 &0.027 &0.034 &0.108 &0.056 &0.057 &0.052 &0.095 &0.092 &0.052 &0.071 &0.067 &0.058 &0.153 &0.067 &0.091 &0.064 &0.073\\ \hline B2 &0.013 &0.025 &0.023 &0.127 &0.015 &0.143 &0.132 &0.132 &0.029 &0.048 &0.061 &0.039 &0.145 &0.153 &0.062 &0.206 &0.108 &0.061 &0.126 &0.138\\ \hline B3 &0.01 &0.015 &0.009 &0.028 &0.007 &0.016 &0.015 &0.014 &0.017 &0.019 &0.023 &0.013 &0.031 &0.087 &0.058 &0.099 &0.02 &0.021 &0.038 &0.017\\ \hline C1 &0.012 &0.014 &0.015 &0.019 &0.013 &0.025 &0.012 &0.014 &0.015 &0.019 &0.021 &0.017 &0.074 &0.056 &0.056 &0.123 &0.016 &0.018 &0.02 &0.023\\ \hline C2 &0.009 &0.021 &0.02 &0.029 &0.021 &0.041 &0.038 &0.02 &0.036 &0.063 &0.081 &0.046 &0.119 &0.12 &0.023 &0.156 &0.039 &0.043 &0.117 &0.04\\ \hline C3 &0.013 &0.025 &0.028 &0.105 &0.033 &0.121 &0.059 &0.056 &0.025 &0.12 &0.112 &0.058 &0.081 &0.087 &0.057 &0.174 &0.131 &0.102 &0.113 &0.095\\ \hline C4 &0.008 &0.016 &0.021 &0.037 &0.014 &0.033 &0.033 &0.028 &0.02 &0.025 &0.032 &0.02 &0.028 &0.028 &0.022 &0.102 &0.027 &0.093 &0.035 &0.095\\ \hline D1 &0.01 &0.016 &0.027 &0.03 &0.014 &0.038 &0.03 &0.031 &0.056 &0.1 &0.024 &0.096 &0.046 &0.034 &0.025 &0.123 &0.125 &0.126 &0.034 &0.044\\ \hline D2 &0.005 &0.011 &0.025 &0.015 &0.01 &0.043 &0.015 &0.031 &0.014 &0.019 &0.018 &0.011 &0.115 &0.021 &0.017 &0.036 &0.022 &0.033 &0.024 &0.022\\ \hline D3 &0.004 &0.01 &0.031 &0.013 &0.009 &0.024 &0.025 &0.02 &0.018 &0.022 &0.023 &0.024 &0.014 &0.016 &0.012 &0.027 &0.021 &0.018 &0.027 &0.021\\ \hline D4 &0.015 &0.054 &0.016 &0.022 &0.012 &0.03 &0.029 &0.025 &0.023 &0.027 &0.033 &0.026 &0.122 &0.02 &0.026 &0.084 &0.04 &0.039 &0.034 &0.038\\ \hline D5 &0.01 &0.011 &0.017 &0.027 &0.012 &0.094 &0.029 &0.03 &0.031 &0.041 &0.041 &0.041 &0.122 &0.029 &0.015 &0.054 &0.032 &0.037 &0.034 &0.032\\ \hline E1 &0.016 &0.029 &0.012 &0.021 &0.011 &0.023 &0.02 &0.018 &0.022 &0.023 &0.042 &0.019 &0.026 &0.022 &0.029 &0.031 &0.038 &0.037 &0.036 &0.038\\ \hline E2 &0.011 &0.013 &0.019 &0.019 &0.012 &0.025 &0.021 &0.032 &0.017 &0.023 &0.023 &0.04 &0.124 &0.058 &0.029 &0.131 &0.017 &0.03 &0.041 &0.04\\ \hline E3 &0.01 &0.02 &0.019 &0.071 &0.017 &0.108 &0.098 &0.096 &0.046 &0.108 &0.049 &0.04 &0.069 &0.1 &0.064 &0.177 &0.07 &0.035 &0.068 &0.058\\ \hline E4 &0.007 &0.018 &0.015 &0.023 &0.013 &0.052 &0.04 &0.037 &0.03 &0.039 &0.036 &0.047 &0.064 &0.038 &0.033 &0.141 &0.026 &0.044 &0.024 &0.081\\ \hline E5 &0.01 &0.02 &0.015 &0.064 &0.014 &0.074 &0.068 &0.066 &0.021 &0.097 &0.034 &0.024 &0.038 &0.037 &0.035 &0.132 &0.028 &0.035 &0.099 &0.029\\ \hline \end{array} $$
影响度、被影响度、中心度、原因度的求解 $$ \begin{CD} T @>>>\{D|C\}@>>>\{M|R \} \\ \end{CD} $$
求解原理
| 影响度 $D$ | $$ D_i=\sum \limits_{j=1}^{n}{t_{ij}},(i=1,2,3,\cdots,n) $$ |
| 被影响度 $C$ | $$ C_i=\sum \limits_{j=1}^{n}{t_{ji}},(i=1,2,3,\cdots,n) $$ |
| 中心度 $M$ | $$ M_i=D_i+C_i $$ |
| 原因度 $ R$ | $$ R_i=D_i-C_i $$ |
结果
影响度、被影响度、中心度、原因度
$$\begin{array}{|c|c|c|c|c|c|c|}\hline {M_{20 \times4}} &Di &Ci &Mi &Ri\\ \hline A1 &1.226 &0.22 &1.446 &1.006\\ \hline A2 &1.563 &0.378 &1.941 &1.185\\ \hline A3 &0.828 &0.404 &1.232 &0.424\\ \hline B1 &1.257 &0.91 &2.168 &0.347\\ \hline B2 &1.786 &0.317 &2.104 &1.469\\ \hline B3 &0.56 &1.239 &1.798 &-0.679\\ \hline C1 &0.582 &0.972 &1.553 &-0.39\\ \hline C2 &1.081 &0.843 &1.924 &0.238\\ \hline C3 &1.596 &0.601 &2.196 &0.995\\ \hline C4 &0.718 &1.049 &1.767 &-0.332\\ \hline D1 &1.03 &1.013 &2.043 &0.016\\ \hline D2 &0.507 &0.846 &1.353 &-0.34\\ \hline D3 &0.379 &1.511 &1.89 &-1.132\\ \hline D4 &0.717 &1.235 &1.952 &-0.518\\ \hline D5 &0.74 &0.864 &1.604 &-0.124\\ \hline E1 &0.512 &2.218 &2.73 &-1.707\\ \hline E2 &0.725 &1.065 &1.789 &-0.34\\ \hline E3 &1.322 &1.001 &2.323 &0.321\\ \hline E4 &0.807 &1.046 &1.853 &-0.24\\ \hline E5 &0.941 &1.141 &2.082 &-0.2\\ \hline \end{array} $$
绘制图表中心度——原因度的图表
从DEMATEL到对抗哈斯图(AHDT)
偏序-序拓扑
偏序( Partial order )其实质就是序拓扑的求解
$$ \begin{CD} D=\left[ d_{ij} \right]_{n \times m}@>偏序规则>>A=\left[a_{ij} \right]_{n \times n} \\ \end{CD} $$
其中 $D=\left[ d_{ij} \right]_{n \times m}$ 为决策评价矩阵。$n$行$m$列。$n$代表评价对象(要素、方案、样本);$m$代表维度(准则、属性、目标)。
其中 $A=\left[ a_{ij} \right]_{n \times n}$ 为关系矩阵。是一个布尔方阵。$n$代表评价对象(要素、方案、样本)。
对于决策矩阵$D$中 $n$个要素的任何一列都具有严格的可比性。
偏序规则
对于含有m列的评价矩阵D,其中的任意一列即指标维度,具有同属性,可比较的前提。维度的这种优劣的比较至少有着两种属性。
数值越大越优,数值越小越差,称之为正向指标。记作p1、p2……pm。 数值越小越好,数值越大越差,称之为负向指标。记作q1、q2……qm。
对于决策矩阵$D$中的任意两行$x,y$
负向指标有 $d_{(x,p1)} \geqslant d_{(y,p1)} 且d_{(x,p2)} \geqslant d_{(y,p2)} 且 {\cdots}且d_{(x,pm)} \geqslant d_{(y,pm)}$ 同时有
正向指标有 $d_{(x,q1)} \leqslant d_{(y,q1)} 且d_{(x,q2)} \leqslant d_{(y,q2)} 且 {\cdots}且d_{(x,qm)} \leqslant d_{(y,qm)}$
符合上述规则,要素$x$与要素$y$的偏序关系记作:$x ≺ y$
$x \prec y$的意义为$y要素$优于(好于,牛逼于,帅于,猛于)$x要素$ 。
上述规则成为偏序规则。对于决策矩阵通过偏序规则可以得到关系矩阵 $A$
$$a_{xy}= \begin{cases} 1, x \prec y \\ 0, 其它 \end{cases} $$
中心度,原因度的意义
中心度,与原因度的绝对值都为正向指标,即的数值越大越重要。
任意两个要素,当其要素X的中心度的数值与原因度的绝对值同时大于另外一个要素Y则有
$Y \prec X$
从决策矩阵到关系矩阵 $$ \begin{CD} D=\left[ d_{ij} \right]_{n \times 2}@>取偏序>>A=\left[a_{ij} \right]_{n \times n} \\ \end{CD} $$
中心度,原因度绝对值组成的决策矩阵D
$$D=\begin{array}{c|c|c|c|c|c|c}{M_{20 \times2}} &M &|R|\\ \hline A1 &1.4461 &1.006\\ \hline A2 &1.9409 &1.1852\\ \hline A3 &1.2316 &0.4243\\ \hline B1 &2.1679 &0.3471\\ \hline B2 &2.1038 &1.469\\ \hline B3 &1.7984 &0.6792\\ \hline C1 &1.5535 &0.3904\\ \hline C2 &1.9236 &0.2378\\ \hline C3 &2.1961 &0.9951\\ \hline C4 &1.7671 &0.3317\\ \hline D1 &2.0429 &0.0161\\ \hline D2 &1.3528 &0.3396\\ \hline D3 &1.8904 &1.1324\\ \hline D4 &1.9518 &0.518\\ \hline D5 &1.6037 &0.1241\\ \hline E1 &2.7301 &1.7068\\ \hline E2 &1.7894 &0.3399\\ \hline E3 &2.3234 &0.321\\ \hline E4 &1.8531 &0.2398\\ \hline E5 &2.0816 &0.1998\\ \hline \end{array} $$关系矩阵$A$
$$A=\begin{array} {c|c|c|c|c|c|c|c}{M_{20 \times20}} &A1 &A2 &A3 &B1 &B2 &B3 &C1 &C2 &C3 &C4 &D1 &D2 &D3 &D4 &D5 &E1 &E2 &E3 &E4 &E5\\ \hline A1 &1 &1 & & &1 & & & & & & & &1 & & &1 & & & & \\ \hline A2 & &1 & & &1 & & & & & & & & & & &1 & & & & \\ \hline A3 &1 &1 &1 & &1 &1 & & &1 & & & &1 &1 & &1 & & & & \\ \hline B1 & & & &1 & & & & &1 & & & & & & &1 & & & & \\ \hline B2 & & & & &1 & & & & & & & & & & &1 & & & & \\ \hline B3 & &1 & & &1 &1 & & &1 & & & &1 & & &1 & & & & \\ \hline C1 & &1 & & &1 &1 &1 & &1 & & & &1 &1 & &1 & & & & \\ \hline C2 & &1 & &1 &1 & & &1 &1 & & & & &1 & &1 & &1 & & \\ \hline C3 & & & & & & & & &1 & & & & & & &1 & & & & \\ \hline C4 & &1 & &1 &1 &1 & & &1 &1 & & &1 &1 & &1 &1 & & & \\ \hline D1 & & & &1 &1 & & & &1 & &1 & & & & &1 & &1 & &1\\ \hline D2 &1 &1 & &1 &1 &1 &1 & &1 & & &1 &1 &1 & &1 &1 & & & \\ \hline D3 & &1 & & &1 & & & & & & & &1 & & &1 & & & & \\ \hline D4 & & & & &1 & & & &1 & & & & &1 & &1 & & & & \\ \hline D5 & &1 & &1 &1 &1 & &1 &1 &1 & & &1 &1 &1 &1 &1 &1 &1 &1\\ \hline E1 & & & & & & & & & & & & & & & &1 & & & & \\ \hline E2 & &1 & &1 &1 &1 & & &1 & & & &1 &1 & &1 &1 & & & \\ \hline E3 & & & & & & & & & & & & & & & &1 & &1 & & \\ \hline E4 & &1 & &1 &1 & & & &1 & & & &1 &1 & &1 & &1 &1 & \\ \hline E5 & & & &1 &1 & & & &1 & & & & & & &1 & &1 & &1\\ \hline \end{array} $$对抗哈斯图(AHDT)部分求解
关系矩阵到相乘矩阵 \begin{CD} A@>A+I>>B \\ \end{CD}
$$B=\begin{array} {c|c|c|c|c|c|c|c}{M_{20 \times20}} &A1 &A2 &A3 &B1 &B2 &B3 &C1 &C2 &C3 &C4 &D1 &D2 &D3 &D4 &D5 &E1 &E2 &E3 &E4 &E5\\ \hline A1 &1 &1 & & &1 & & & & & & & &1 & & &1 & & & & \\ \hline A2 & &1 & & &1 & & & & & & & & & & &1 & & & & \\ \hline A3 &1 &1 &1 & &1 &1 & & &1 & & & &1 &1 & &1 & & & & \\ \hline B1 & & & &1 & & & & &1 & & & & & & &1 & & & & \\ \hline B2 & & & & &1 & & & & & & & & & & &1 & & & & \\ \hline B3 & &1 & & &1 &1 & & &1 & & & &1 & & &1 & & & & \\ \hline C1 & &1 & & &1 &1 &1 & &1 & & & &1 &1 & &1 & & & & \\ \hline C2 & &1 & &1 &1 & & &1 &1 & & & & &1 & &1 & &1 & & \\ \hline C3 & & & & & & & & &1 & & & & & & &1 & & & & \\ \hline C4 & &1 & &1 &1 &1 & & &1 &1 & & &1 &1 & &1 &1 & & & \\ \hline D1 & & & &1 &1 & & & &1 & &1 & & & & &1 & &1 & &1\\ \hline D2 &1 &1 & &1 &1 &1 &1 & &1 & & &1 &1 &1 & &1 &1 & & & \\ \hline D3 & &1 & & &1 & & & & & & & &1 & & &1 & & & & \\ \hline D4 & & & & &1 & & & &1 & & & & &1 & &1 & & & & \\ \hline D5 & &1 & &1 &1 &1 & &1 &1 &1 & & &1 &1 &1 &1 &1 &1 &1 &1\\ \hline E1 & & & & & & & & & & & & & & & &1 & & & & \\ \hline E2 & &1 & &1 &1 &1 & & &1 & & & &1 &1 & &1 &1 & & & \\ \hline E3 & & & & & & & & & & & & & & & &1 & &1 & & \\ \hline E4 & &1 & &1 &1 & & & &1 & & & &1 &1 & &1 & &1 &1 & \\ \hline E5 & & & &1 &1 & & & &1 & & & & & & &1 & &1 & &1\\ \hline \end{array} $$
相乘矩阵B到可达矩阵R \begin{CD} B@>连乘或者幂乘>>R \\ \end{CD}
可达矩阵R
$$R=\begin{array} {c|c|c|c|c|c|c|c}{M_{20 \times20}} &A1 &A2 &A3 &B1 &B2 &B3 &C1 &C2 &C3 &C4 &D1 &D2 &D3 &D4 &D5 &E1 &E2 &E3 &E4 &E5\\ \hline A1 &1 &1 & & &1 & & & & & & & &1 & & &1 & & & & \\ \hline A2 & &1 & & &1 & & & & & & & & & & &1 & & & & \\ \hline A3 &1 &1 &1 & &1 &1 & & &1 & & & &1 &1 & &1 & & & & \\ \hline B1 & & & &1 & & & & &1 & & & & & & &1 & & & & \\ \hline B2 & & & & &1 & & & & & & & & & & &1 & & & & \\ \hline B3 & &1 & & &1 &1 & & &1 & & & &1 & & &1 & & & & \\ \hline C1 & &1 & & &1 &1 &1 & &1 & & & &1 &1 & &1 & & & & \\ \hline C2 & &1 & &1 &1 & & &1 &1 & & & & &1 & &1 & &1 & & \\ \hline C3 & & & & & & & & &1 & & & & & & &1 & & & & \\ \hline C4 & &1 & &1 &1 &1 & & &1 &1 & & &1 &1 & &1 &1 & & & \\ \hline D1 & & & &1 &1 & & & &1 & &1 & & & & &1 & &1 & &1\\ \hline D2 &1 &1 & &1 &1 &1 &1 & &1 & & &1 &1 &1 & &1 &1 & & & \\ \hline D3 & &1 & & &1 & & & & & & & &1 & & &1 & & & & \\ \hline D4 & & & & &1 & & & &1 & & & & &1 & &1 & & & & \\ \hline D5 & &1 & &1 &1 &1 & &1 &1 &1 & & &1 &1 &1 &1 &1 &1 &1 &1\\ \hline E1 & & & & & & & & & & & & & & & &1 & & & & \\ \hline E2 & &1 & &1 &1 &1 & & &1 & & & &1 &1 & &1 &1 & & & \\ \hline E3 & & & & & & & & & & & & & & & &1 & &1 & & \\ \hline E4 & &1 & &1 &1 & & & &1 & & & &1 &1 & &1 & &1 &1 & \\ \hline E5 & & & &1 &1 & & & &1 & & & & & & &1 & &1 & &1\\ \hline \end{array} $$由可达矩阵通过对抗的抽取方式得到一对要素的层级分布 \begin{CD} R @>结果优先抽取>原因优先抽取> \frac {up型要素层级分布 }{down 型要素层级分布} \\ \end{CD}
可达矩阵R层级抽取的过程如下
| 结果优先——UP型抽取过程 | 原因优先——DOWN型抽取过程 |
| $$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline A1 &A1 ,A2 ,B2 ,D3 ,E1 &A1 \\\hline A2 &A2 ,B2 ,E1 &A2 \\\hline A3 &A1 ,A2 ,A3 ,B2 ,B3 ,C3 ,D3 ,D4 ,E1 &A3 \\\hline B1 &B1 ,C3 ,E1 &B1 \\\hline B2 &B2 ,E1 &B2 \\\hline B3 &A2 ,B2 ,B3 ,C3 ,D3 ,E1 &B3 \\\hline C1 &A2 ,B2 ,B3 ,C1 ,C3 ,D3 ,D4 ,E1 &C1 \\\hline C2 &A2 ,B1 ,B2 ,C2 ,C3 ,D4 ,E1 ,E3 &C2 \\\hline C3 &C3 ,E1 &C3 \\\hline C4 &A2 ,B1 ,B2 ,B3 ,C3 ,C4 ,D3 ,D4 ,E1 ,E2 &C4 \\\hline D1 &B1 ,B2 ,C3 ,D1 ,E1 ,E3 ,E5&D1 \\\hline D2 &A1 ,A2 ,B1 ,B2 ,B3 ,C1 ,C3 ,D2 ,D3 ,D4 ,E1 ,E2 &D2 \\\hline D3 &A2 ,B2 ,D3 ,E1 &D3 \\\hline D4 &B2 ,C3 ,D4 ,E1 &D4 \\\hline D5 &A2 ,B1 ,B2 ,B3 ,C2 ,C3 ,C4 ,D3 ,D4 ,D5 ,E1 ,E2 ,E3 ,E4 ,E5&D5 \\\hline E1 &\color{red}{\fbox{E1 }}&\color{red}{\fbox{E1 }} \\\hline E2 &A2 ,B1 ,B2 ,B3 ,C3 ,D3 ,D4 ,E1 ,E2 &E2 \\\hline E3 &E1 ,E3 &E3 \\\hline E4 &A2 ,B1 ,B2 ,C3 ,D3 ,D4 ,E1 ,E3 ,E4 &E4 \\\hline E5&B1 ,B2 ,C3 ,E1 ,E3 ,E5&E5 \\\hline \end{array} $$ | $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline A1 &A1 ,A3 ,D2 &A1 \\\hline A2 &A1 ,A2 ,A3 ,B3 ,C1 ,C2 ,C4 ,D2 ,D3 ,D5 ,E2 ,E4 &A2 \\\hline A3 &\color{blue}{\fbox{A3 }}&\color{blue}{\fbox{A3 }} \\\hline B1 &B1 ,C2 ,C4 ,D1 ,D2 ,D5 ,E2 ,E4 ,E5&B1 \\\hline B2 &A1 ,A2 ,A3 ,B2 ,B3 ,C1 ,C2 ,C4 ,D1 ,D2 ,D3 ,D4 ,D5 ,E2 ,E4 ,E5&B2 \\\hline B3 &A3 ,B3 ,C1 ,C4 ,D2 ,D5 ,E2 &B3 \\\hline C1 &C1 ,D2 &C1 \\\hline C2 &C2 ,D5 &C2 \\\hline C3 &A3 ,B1 ,B3 ,C1 ,C2 ,C3 ,C4 ,D1 ,D2 ,D4 ,D5 ,E2 ,E4 ,E5&C3 \\\hline C4 &C4 ,D5 &C4 \\\hline D1 &\color{blue}{\fbox{D1 }}&\color{blue}{\fbox{D1 }} \\\hline D2 &\color{blue}{\fbox{D2 }}&\color{blue}{\fbox{D2 }} \\\hline D3 &A1 ,A3 ,B3 ,C1 ,C4 ,D2 ,D3 ,D5 ,E2 ,E4 &D3 \\\hline D4 &A3 ,C1 ,C2 ,C4 ,D2 ,D4 ,D5 ,E2 ,E4 &D4 \\\hline D5 &\color{blue}{\fbox{D5 }}&\color{blue}{\fbox{D5 }} \\\hline E1 &A1 ,A2 ,A3 ,B1 ,B2 ,B3 ,C1 ,C2 ,C3 ,C4 ,D1 ,D2 ,D3 ,D4 ,D5 ,E1 ,E2 ,E3 ,E4 ,E5&E1 \\\hline E2 &C4 ,D2 ,D5 ,E2 &E2 \\\hline E3 &C2 ,D1 ,D5 ,E3 ,E4 ,E5&E3 \\\hline E4 &D5 ,E4 &E4 \\\hline E5&D1 ,D5 ,E5&E5 \\\hline \end{array} $$ |
| 抽取出E1 放置上层,删除后剩余的情况如下 | 抽取出A3 ,D1 ,D2 ,D5 放置下层,删除后剩余的情况如下 |
| $$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline A1 &A1 ,A2 ,B2 ,D3 &A1 \\\hline A2 &A2 ,B2 &A2 \\\hline A3 &A1 ,A2 ,A3 ,B2 ,B3 ,C3 ,D3 ,D4 &A3 \\\hline B1 &B1 ,C3 &B1 \\\hline B2 &\color{red}{\fbox{B2 }}&\color{red}{\fbox{B2 }} \\\hline B3 &A2 ,B2 ,B3 ,C3 ,D3 &B3 \\\hline C1 &A2 ,B2 ,B3 ,C1 ,C3 ,D3 ,D4 &C1 \\\hline C2 &A2 ,B1 ,B2 ,C2 ,C3 ,D4 ,E3 &C2 \\\hline C3 &\color{red}{\fbox{C3 }}&\color{red}{\fbox{C3 }} \\\hline C4 &A2 ,B1 ,B2 ,B3 ,C3 ,C4 ,D3 ,D4 ,E2 &C4 \\\hline D1 &B1 ,B2 ,C3 ,D1 ,E3 ,E5&D1 \\\hline D2 &A1 ,A2 ,B1 ,B2 ,B3 ,C1 ,C3 ,D2 ,D3 ,D4 ,E2 &D2 \\\hline D3 &A2 ,B2 ,D3 &D3 \\\hline D4 &B2 ,C3 ,D4 &D4 \\\hline D5 &A2 ,B1 ,B2 ,B3 ,C2 ,C3 ,C4 ,D3 ,D4 ,D5 ,E2 ,E3 ,E4 ,E5&D5 \\\hline E2 &A2 ,B1 ,B2 ,B3 ,C3 ,D3 ,D4 ,E2 &E2 \\\hline E3 &\color{red}{\fbox{E3 }}&\color{red}{\fbox{E3 }} \\\hline E4 &A2 ,B1 ,B2 ,C3 ,D3 ,D4 ,E3 ,E4 &E4 \\\hline E5&B1 ,B2 ,C3 ,E3 ,E5&E5 \\\hline \end{array} $$ | $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline A1 &\color{blue}{\fbox{A1 }}&\color{blue}{\fbox{A1 }} \\\hline A2 &A1 ,A2 ,B3 ,C1 ,C2 ,C4 ,D3 ,E2 ,E4 &A2 \\\hline B1 &B1 ,C2 ,C4 ,E2 ,E4 ,E5&B1 \\\hline B2 &A1 ,A2 ,B2 ,B3 ,C1 ,C2 ,C4 ,D3 ,D4 ,E2 ,E4 ,E5&B2 \\\hline B3 &B3 ,C1 ,C4 ,E2 &B3 \\\hline C1 &\color{blue}{\fbox{C1 }}&\color{blue}{\fbox{C1 }} \\\hline C2 &\color{blue}{\fbox{C2 }}&\color{blue}{\fbox{C2 }} \\\hline C3 &B1 ,B3 ,C1 ,C2 ,C3 ,C4 ,D4 ,E2 ,E4 ,E5&C3 \\\hline C4 &\color{blue}{\fbox{C4 }}&\color{blue}{\fbox{C4 }} \\\hline D3 &A1 ,B3 ,C1 ,C4 ,D3 ,E2 ,E4 &D3 \\\hline D4 &C1 ,C2 ,C4 ,D4 ,E2 ,E4 &D4 \\\hline E1 &A1 ,A2 ,B1 ,B2 ,B3 ,C1 ,C2 ,C3 ,C4 ,D3 ,D4 ,E1 ,E2 ,E3 ,E4 ,E5&E1 \\\hline E2 &C4 ,E2 &E2 \\\hline E3 &C2 ,E3 ,E4 ,E5&E3 \\\hline E4 &\color{blue}{\fbox{E4 }}&\color{blue}{\fbox{E4 }} \\\hline E5&\color{blue}{\fbox{E5}}&\color{blue}{\fbox{E5}} \\\hline \end{array} $$ |
| 抽取出B2 、C3 、E3 放置上层,删除后剩余的情况如下 | 抽取出A1 ,C1 ,C2 ,C4 ,E4 ,E5放置下层,删除后剩余的情况如下 |
| $$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline A1 &A1 ,A2 ,D3 &A1 \\\hline A2 &\color{red}{\fbox{A2 }}&\color{red}{\fbox{A2 }} \\\hline A3 &A1 ,A2 ,A3 ,B3 ,D3 ,D4 &A3 \\\hline B1 &\color{red}{\fbox{B1 }}&\color{red}{\fbox{B1 }} \\\hline B3 &A2 ,B3 ,D3 &B3 \\\hline C1 &A2 ,B3 ,C1 ,D3 ,D4 &C1 \\\hline C2 &A2 ,B1 ,C2 ,D4 &C2 \\\hline C4 &A2 ,B1 ,B3 ,C4 ,D3 ,D4 ,E2 &C4 \\\hline D1 &B1 ,D1 ,E5&D1 \\\hline D2 &A1 ,A2 ,B1 ,B3 ,C1 ,D2 ,D3 ,D4 ,E2 &D2 \\\hline D3 &A2 ,D3 &D3 \\\hline D4 &\color{red}{\fbox{D4 }}&\color{red}{\fbox{D4 }} \\\hline D5 &A2 ,B1 ,B3 ,C2 ,C4 ,D3 ,D4 ,D5 ,E2 ,E4 ,E5&D5 \\\hline E2 &A2 ,B1 ,B3 ,D3 ,D4 ,E2 &E2 \\\hline E4 &A2 ,B1 ,D3 ,D4 ,E4 &E4 \\\hline E5&B1 ,E5&E5 \\\hline \end{array} $$ | $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline A2 &A2 ,B3 ,D3 ,E2 &A2 \\\hline B1 &B1 ,E2 &B1 \\\hline B2 &A2 ,B2 ,B3 ,D3 ,D4 ,E2 &B2 \\\hline B3 &B3 ,E2 &B3 \\\hline C3 &B1 ,B3 ,C3 ,D4 ,E2 &C3 \\\hline D3 &B3 ,D3 ,E2 &D3 \\\hline D4 &D4 ,E2 &D4 \\\hline E1 &A2 ,B1 ,B2 ,B3 ,C3 ,D3 ,D4 ,E1 ,E2 ,E3 &E1 \\\hline E2 &\color{blue}{\fbox{E2 }}&\color{blue}{\fbox{E2 }} \\\hline E3 &\color{blue}{\fbox{E3 }}&\color{blue}{\fbox{E3 }} \\\hline \end{array} $$ |
| 抽取出A2 、B1 、D4 放置上层,删除后剩余的情况如下 | 抽取出E2 ,E3 放置下层,删除后剩余的情况如下 |
| $$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline A1 &A1 ,D3 &A1 \\\hline A3 &A1 ,A3 ,B3 ,D3 &A3 \\\hline B3 &B3 ,D3 &B3 \\\hline C1 &B3 ,C1 ,D3 &C1 \\\hline C2 &\color{red}{\fbox{C2 }}&\color{red}{\fbox{C2 }} \\\hline C4 &B3 ,C4 ,D3 ,E2 &C4 \\\hline D1 &D1 ,E5&D1 \\\hline D2 &A1 ,B3 ,C1 ,D2 ,D3 ,E2 &D2 \\\hline D3 &\color{red}{\fbox{D3 }}&\color{red}{\fbox{D3 }} \\\hline D5 &B3 ,C2 ,C4 ,D3 ,D5 ,E2 ,E4 ,E5&D5 \\\hline E2 &B3 ,D3 ,E2 &E2 \\\hline E4 &D3 ,E4 &E4 \\\hline E5&\color{red}{\fbox{E5}}&\color{red}{\fbox{E5}} \\\hline \end{array} $$ | $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline A2 &A2 ,B3 ,D3 &A2 \\\hline B1 &\color{blue}{\fbox{B1 }}&\color{blue}{\fbox{B1 }} \\\hline B2 &A2 ,B2 ,B3 ,D3 ,D4 &B2 \\\hline B3 &\color{blue}{\fbox{B3 }}&\color{blue}{\fbox{B3 }} \\\hline C3 &B1 ,B3 ,C3 ,D4 &C3 \\\hline D3 &B3 ,D3 &D3 \\\hline D4 &\color{blue}{\fbox{D4 }}&\color{blue}{\fbox{D4 }} \\\hline E1 &A2 ,B1 ,B2 ,B3 ,C3 ,D3 ,D4 ,E1 &E1 \\\hline \end{array} $$ |
| 抽取出C2 、D3 、E5放置上层,删除后剩余的情况如下 | 抽取出B1 ,B3 ,D4 放置下层,删除后剩余的情况如下 |
| $$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline A1 &\color{red}{\fbox{A1 }}&\color{red}{\fbox{A1 }} \\\hline A3 &A1 ,A3 ,B3 &A3 \\\hline B3 &\color{red}{\fbox{B3 }}&\color{red}{\fbox{B3 }} \\\hline C1 &B3 ,C1 &C1 \\\hline C4 &B3 ,C4 ,E2 &C4 \\\hline D1 &\color{red}{\fbox{D1 }}&\color{red}{\fbox{D1 }} \\\hline D2 &A1 ,B3 ,C1 ,D2 ,E2 &D2 \\\hline D5 &B3 ,C4 ,D5 ,E2 ,E4 &D5 \\\hline E2 &B3 ,E2 &E2 \\\hline E4 &\color{red}{\fbox{E4 }}&\color{red}{\fbox{E4 }} \\\hline \end{array} $$ | $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline A2 &A2 ,D3 &A2 \\\hline B2 &A2 ,B2 ,D3 &B2 \\\hline C3 &\color{blue}{\fbox{C3 }}&\color{blue}{\fbox{C3 }} \\\hline D3 &\color{blue}{\fbox{D3 }}&\color{blue}{\fbox{D3 }} \\\hline E1 &A2 ,B2 ,C3 ,D3 ,E1 &E1 \\\hline \end{array} $$ |
| 抽取出A1 、B3 、D1 、E4 放置上层,删除后剩余的情况如下 | 抽取出C3 ,D3 放置下层,删除后剩余的情况如下 |
| $$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline A3 &\color{red}{\fbox{A3 }}&\color{red}{\fbox{A3 }} \\\hline C1 &\color{red}{\fbox{C1 }}&\color{red}{\fbox{C1 }} \\\hline C4 &C4 ,E2 &C4 \\\hline D2 &C1 ,D2 ,E2 &D2 \\\hline D5 &C4 ,D5 ,E2 &D5 \\\hline E2 &\color{red}{\fbox{E2 }}&\color{red}{\fbox{E2 }} \\\hline \end{array} $$ | $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline A2 &\color{blue}{\fbox{A2 }}&\color{blue}{\fbox{A2 }} \\\hline B2 &A2 ,B2 &B2 \\\hline E1 &A2 ,B2 ,E1 &E1 \\\hline \end{array} $$ |
| 抽取出A3 、C1 、E2 放置上层,删除后剩余的情况如下 | 抽取出A2 放置下层,删除后剩余的情况如下 |
| $$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline C4 &\color{red}{\fbox{C4 }}&\color{red}{\fbox{C4 }} \\\hline D2 &\color{red}{\fbox{D2 }}&\color{red}{\fbox{D2 }} \\\hline D5 &C4 ,D5 &D5 \\\hline \end{array} $$ | $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline B2 &\color{blue}{\fbox{B2 }}&\color{blue}{\fbox{B2 }} \\\hline E1 &B2 ,E1 &E1 \\\hline \end{array} $$ |
| 抽取出C4 、D2 放置上层,删除后剩余的情况如下 | 抽取出B2 放置下层,删除后剩余的情况如下 |
| $$\begin{array} {c|c|c|c|c|c|c|c}{} & R_{e} & T_{e} \\\hline D5 &\color{red}{\fbox{D5 }}&\color{red}{\fbox{D5 }} \\\hline \end{array} $$ | $$\begin{array} {c|c|c|c|c|c|c|c}{} &Q_{e} & T_{e} \\\hline E1 &\color{blue}{\fbox{E1 }}&\color{blue}{\fbox{E1 }} \\\hline \end{array} $$ |
| 抽取出D5 放置上层,删除后剩余的情况如下 | 抽取出E1 放置下层,删除后剩余的情况如下 |
抽取方式的结果如下
| 层级 | 结果优先——UP型 | 原因优先——DOWN型 |
| 第0层 | E1 | E1 |
| 第1层 | B2 ,C3 ,E3 | B2 |
| 第2层 | A2 ,B1 ,D4 | A2 |
| 第3层 | C2 ,D3 ,E5 | C3 ,D3 |
| 第4层 | A1 ,B3 ,D1 ,E4 | B1 ,B3 ,D4 |
| 第5层 | A3 ,C1 ,E2 | E2 ,E3 |
| 第6层 | C4 ,D2 | A1 ,C1 ,C2 ,C4 ,E4 ,E5 |
| 第7层 | D5 | A3 ,D1 ,D2 ,D5 |
计算一般性骨架矩阵 \begin{CD} R @>缩点运算>>R' @>缩边运算>>S' @>以最简菊花链表示回路>>S \\ \end{CD}
一般性骨架矩阵即为不缩点的情况下的最简结构,即边数最少。$S$如下
$$S=\begin{array} {c|c|c|c|c|c|c|c}{M_{20 \times20}} &A1 &A2 &A3 &B1 &B2 &B3 &C1 &C2 &C3 &C4 &D1 &D2 &D3 &D4 &D5 &E1 &E2 &E3 &E4 &E5\\ \hline A1 & & & & & & & & & & & & &1 & & & & & & & \\ \hline A2 & & & & &1 & & & & & & & & & & & & & & & \\ \hline A3 &1 & & & & &1 & & & & & & & &1 & & & & & & \\ \hline B1 & & & & & & & & &1 & & & & & & & & & & & \\ \hline B2 & & & & & & & & & & & & & & & &1 & & & & \\ \hline B3 & & & & & & & & &1 & & & &1 & & & & & & & \\ \hline C1 & & & & & &1 & & & & & & & &1 & & & & & & \\ \hline C2 & &1 & &1 & & & & & & & & & &1 & & & &1 & & \\ \hline C3 & & & & & & & & & & & & & & & &1 & & & & \\ \hline C4 & & & & & & & & & & & & & & & & &1 & & & \\ \hline D1 & & & & & & & & & & & & & & & & & & & &1\\ \hline D2 &1 & & & & & &1 & & & & & & & & & &1 & & & \\ \hline D3 & &1 & & & & & & & & & & & & & & & & & & \\ \hline D4 & & & & &1 & & & &1 & & & & & & & & & & & \\ \hline D5 & & & & & & & &1 & &1 & & & & & & & & &1 &1\\ \hline E1 & & & & & & & & & & & & & & & & & & & & \\ \hline E2 & & & &1 & &1 & & & & & & & &1 & & & & & & \\ \hline E3 & & & & & & & & & & & & & & & &1 & & & & \\ \hline E4 & & & &1 & & & & & & & & &1 &1 & & & &1 & & \\ \hline E5 & & & &1 &1 & & & & & & & & & & & & &1 & & \\ \hline \end{array} $$代入一般性骨架矩阵$S$,绘制一组含有权重的对抗层级拓扑图
权重系列求解
$$ \begin{CD} \{M|R \}@>>> d @>>>\omega \\ \end{CD} $$
$ \{M|R \}$ 为要素的中心度与原因度
$d$ 两者合成距离向量
$ \omega $ 权重
求解原理
$$MR=\begin{array}{c|c|c|c|c|c|c}{M_{20 \times2}} &中心度 &原因度\\ \hline A1 &1.4461 &1.006\\ \hline A2 &1.9409 &1.1852\\ \hline A3 &1.2316 &0.4243\\ \hline B1 &2.1679 &0.3471\\ \hline B2 &2.1038 &1.469\\ \hline B3 &1.7984 &0.6792\\ \hline C1 &1.5535 &0.3904\\ \hline C2 &1.9236 &0.2378\\ \hline C3 &2.1961 &0.9951\\ \hline C4 &1.7671 &0.3317\\ \hline D1 &2.0429 &0.0161\\ \hline D2 &1.3528 &0.3396\\ \hline D3 &1.8904 &1.1324\\ \hline D4 &1.9518 &0.518\\ \hline D5 &1.6037 &0.1241\\ \hline E1 &2.7301 &1.7068\\ \hline E2 &1.7894 &0.3399\\ \hline E3 &2.3234 &0.321\\ \hline E4 &1.8531 &0.2398\\ \hline E5 &2.0816 &0.1998\\ \hline \end{array} $$
向量的计算采用欧式距离公式
$$d=\begin{array}{c|c|c|c|c|c|c}{M_{20 \times1}} &向量\\ \hline A1 &1.7616\\ \hline A2 &2.2742\\ \hline A3 &1.3027\\ \hline B1 &2.1955\\ \hline B2 &2.5659\\ \hline B3 &1.9224\\ \hline C1 &1.6018\\ \hline C2 &1.9383\\ \hline C3 &2.4111\\ \hline C4 &1.798\\ \hline D1 &2.043\\ \hline D2 &1.3948\\ \hline D3 &2.2037\\ \hline D4 &2.0194\\ \hline D5 &1.6084\\ \hline E1 &3.2197\\ \hline E2 &1.8214\\ \hline E3 &2.3454\\ \hline E4 &1.8685\\ \hline E5 &2.0912\\ \hline \end{array} $$归一化求权重
$$\omega =\begin{array}{c|c|c|c|c|c|c}{M_{20 \times1}} &权重\\ \hline A1 &0.0436\\ \hline A2 &0.0563\\ \hline A3 &0.0323\\ \hline B1 &0.0544\\ \hline B2 &0.0635\\ \hline B3 &0.0476\\ \hline C1 &0.0397\\ \hline C2 &0.048\\ \hline C3 &0.0597\\ \hline C4 &0.0445\\ \hline D1 &0.0506\\ \hline D2 &0.0345\\ \hline D3 &0.0546\\ \hline D4 &0.05\\ \hline D5 &0.0398\\ \hline E1 &0.0797\\ \hline E2 &0.0451\\ \hline E3 &0.0581\\ \hline E4 &0.0463\\ \hline E5 &0.0518\\ \hline \end{array} $$归一化求子系统的权重
$$\omega =\begin{array}{c|c|c|c|c|c|c}{M_{5 \times1}} &权重\\ \hline A &0.1322\\ \hline B &0.1655\\ \hline C &0.1919\\ \hline D &0.2295\\ \hline E &0.2809\\ \hline \end{array} $$DEMATEL-AHDT核心步骤
偏序部分一定要讲得清楚,尤其是正向指标,负向指标的意思 \begin{CD} D@>取偏序>>A \\ \end{CD}
一般性骨架矩阵的求解
DEMATEL-AHDT编程与计算难点
逆矩阵的求解,即规范化矩阵到综合影响矩阵的过程 \begin{CD} N@>N(I-N)^{-1} >>T \\ \end{CD} \begin{CD} N@>\frac {N}{(I-N)} >>T \\ \end{CD}
一般性骨架矩阵的求解 \begin{CD} R @>缩点运算>>R' @>缩边运算>>S' @>以最简菊花链表示回路增点运算>>S \\ \end{CD}
拓扑图形的拖拽
论文写作要点-原始数据的来源
其它都不是最重要的,因为只要原始数据确定了,整个计算是按部就班的。结果是确定的。因此原始矩阵O的来源最重要,而且按照这一套很难调数据的。
目前用DEMATEL跟ISM方法联用的论文90%是错的,各种错。其中算错的比例最多。而DEMATEL跟AHDT的论文没有,需要讲清楚偏序 \begin{CD} \{ M|R\}@>>>A \\ \end{CD} 这步开始
论文写作要点-对抗层级拓扑图的画法
1、一对层级拓扑图并排一起画,能形成对比,看得一目了然
2、有向边用直的,不要拐弯,不要用组织结构那种。
3、两个图边上加上一个由下至上的箭头,并在底下写原因上面写结果;或者是下面写劣上面写优。
4、活动要素标上颜色,这样人能一下子就注意到
5、回路的画法是重点,请留意回路要素的菊花链画法
6、不需要把文字丢到图里面,不用去凑字数
7、非活动要素,在两边的位置要一致。这样看活动要素看得清楚
8、层级加上,最上层最好是0层,这样显得你是写程序的
9、UP-DOWN可以改成凸——凹等等,注意一定要跟结果优先,原因优先的层级抽取对应起来。
论文写作要点-结果解释
1、活动系统还是刚性系统的解释。
2、活动系统的话,解释活动要素有那些
3、层级的话,可以分为三种类型的要素,结果要素 即是结果要素又是原因要素 ,原因要素
最上层取并集得到的就是 结果要素。
最下层取并集得到的就是原因要素
4、有多少个回路吹下水
论文写作要点-不要瞎改的字母
1、单位矩阵 $I$ 这个不要瞎搞,改成别的一看你就不专业,是抄一篇弱鸡的或者是错的论文
2、可达矩阵 $R$
3、规范化矩阵 $N$
4、综合影响矩阵$T$